Difference between revisions of "005 Sample Final A, Question 16"

Revision as of 10:27, 2 June 2015

Question Graph the following,

-x^{2}+4y^{2}-2x-16y+11=0

Foundations:
1) What type of function is this?
2) What can you say about the orientation of the graph?
Answer:
1) Since both x and y are squared it must be a hyperbola or an ellipse. We can conclude that the graph is a hyperbola since $x^{2}$ and $y^{2}$ have the different signs, one negative and one positive.
2) Since the $y^{2}$ is positive, the hyperbola opens up and down.

Solution:

Step 1:
We start by completing the square twice, once for x and once for y. After completing the squares we end up with $-(x+1)^{2}+4(y-2)^{2}=4$
Common Mistake: When completing the square we will end up adding numbers inside of parenthesis. So make sure you add the correct value to this other side. In this case we add -1, and 16 for completing the square with respect to x and y, respectively.

Step 2:
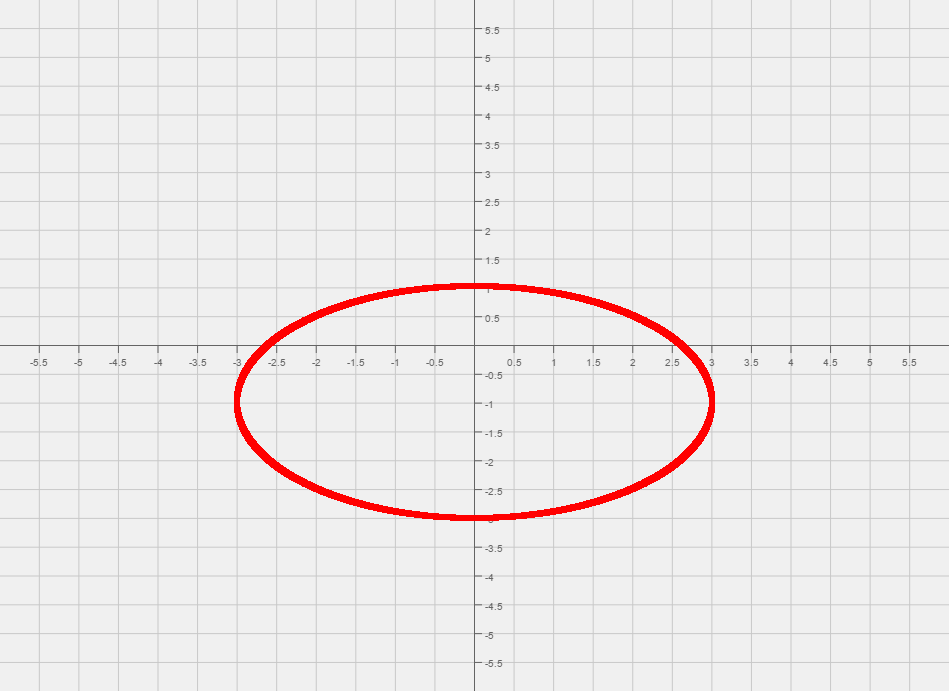
Now that we have the equation that looks like an ellipse, we can read off the center of the ellipse, (0, -1).
From the center mark the two points that are 3 units left, and three units right of the center.
Then mark the two points that are 2 units up, and two units down from the center.

Final Answer:
The four vertices are: $(-3,-1),(3,-1),(0,1){\text{ and }}(0,-3)$

@@ Line 10: / Line 10: @@
 |Answer:
 |-
-|1) Since both x and y are squared it must be a hyperbola or an ellipse. We can conclude that the graph is an ellipse since both <math>x^2</math> &nbsp; and &nbsp; <math>y^2</math> have the same sign, positive.
+|1) Since both x and y are squared it must be a hyperbola or an ellipse. We can conclude that the graph is a hyperbola since <math>x^2</math> &nbsp; and &nbsp; <math>y^2</math> have the different signs, one negative and one positive.
 |-
-|2) Since the coefficient of the <math>x^2</math> term is smaller, when we divide both sides by 36 the X-axis will be the major axis.
+|2) Since the <math>y^2</math> is positive, the hyperbola opens up and down.
 |}
@@ Line 20: / Line 20: @@
 ! Step 1: &nbsp;
 |-
-|We start by dividing both sides by 36. This yields <math>\frac{4x^2}{36} + \frac{9(y + 1)^2}{36} = \frac{x^2}{9} + \frac{(y+1)^2}{4} = 1</math>.
+|We start by completing the square twice, once for x and once for y. After completing the squares we end up with <math>-(x + 1)^2 +4(y - 2)^2 = 4</math>
+|-
+|'''Common Mistake:''' When completing the square we will end up adding numbers inside of parenthesis. So make sure you add the correct value to this other side. In this case we add -1, and 16 for completing the square with respect to x and y, respectively.
 |}