Difference between revisions of "004 Sample Final A, Problem 4"
Jump to navigation
Jump to search
(Created page with "<span class="exam"> Graph the system of inequalities. <math>y > 2x - 3 \qquad y \le 4-x^2</math> {| class="mw-collapsible mw-collapsed" style = "text-align:left;" ! Foundation...") |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
<span class="exam"> Graph the system of inequalities. <math>y > 2x - 3 \qquad y \le 4-x^2</math> | <span class="exam"> Graph the system of inequalities. <math>y > 2x - 3 \qquad y \le 4-x^2</math> | ||
| + | Solution: | ||
| + | |||
{| class="mw-collapsible mw-collapsed" style = "text-align:left;" | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| − | ! | + | ! Step 1: |
|- | |- | ||
| − | | | + | |First we replace the inequalities with equality. So <math>y = 2x - 3</math>, and <math>y = 4 - x^2</math>. |
|- | |- | ||
| − | | | + | |Now we graph both functions. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | |
| − | + | ! Step 2: | |
| − | |||
| − | {| class = "mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| − | ! Step | ||
|- | |- | ||
| − | | | + | |Now that we have graphed both functions we need to know which region to shade with respect to each graph. |
|- | |- | ||
| − | | | + | |To do this we pick a point an equation and a point not on the graph of that equation. We then check if the |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |point satisfies the inequality or not. For both equations we will pick the origin. |
|- | |- | ||
| − | | | + | |<math>y > 2x - 3:</math> Plugging in the origin we get, <math> 0 > 2(0) - 3 = -3 </math>. Since the inequality is false, we shade the side of |
|- | |- | ||
| − | | | + | |<math>y = 2x - 3</math> that does not include the origin. We make the graph of <math>y < \vert x\vert + 1</math> dashed, since the inequality is strict. |
|- | |- | ||
| − | | | + | |<math>y \le 4 - x^2:</math> Plugging in the origin we get <math>0 \le 4 - (0)^2 = 4</math>. Since this inequality is true, we shade the side of <math>y = 4 - x^2</math> that includes the origin. Here we make the graph of <math> y = 4 - x^2 </math> solid since the inequality sign is <math>\le</math> |
|} | |} | ||
| − | {|class = "mw-collapsible mw-collapsed" style = "text-align:left;" | + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" |
| − | ! | + | ! Final Answer: |
|- | |- | ||
| − | | | + | |The final solution is the portion of the graph that below <math>y = 4 - x^2</math> and above <math> y = 2x - 3</math> |
|- | |- | ||
| − | | | + | |The region we are referring to is shaded both blue and red. |
|- | |- | ||
| − | | | + | |[[File:4_Sample_Final_4.png]] |
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[004 Sample Final A|<u>'''Return to Sample Exam</u>''']] | [[004 Sample Final A|<u>'''Return to Sample Exam</u>''']] | ||
Latest revision as of 09:08, 2 June 2015
Graph the system of inequalities. Solution:
| Step 1: |
|---|
| First we replace the inequalities with equality. So , and . |
| Now we graph both functions. |
| Step 2: |
|---|
| Now that we have graphed both functions we need to know which region to shade with respect to each graph. |
| To do this we pick a point an equation and a point not on the graph of that equation. We then check if the |
| point satisfies the inequality or not. For both equations we will pick the origin. |
| Plugging in the origin we get, . Since the inequality is false, we shade the side of |
| that does not include the origin. We make the graph of dashed, since the inequality is strict. |
| Plugging in the origin we get . Since this inequality is true, we shade the side of that includes the origin. Here we make the graph of solid since the inequality sign is |
| Final Answer: |
|---|
| The final solution is the portion of the graph that below and above |
| The region we are referring to is shaded both blue and red. |
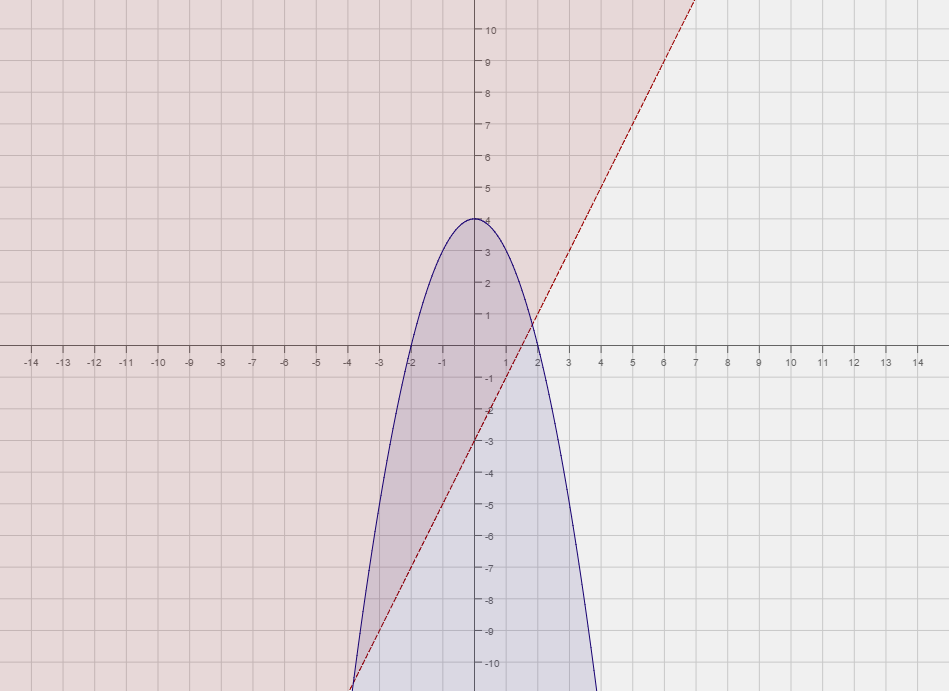
|








