Difference between revisions of "Math 22 Graph of Equation"
| (6 intermediate revisions by the same user not shown) | |||
| Line 32: | Line 32: | ||
To find <math>y</math>-intercepts, let <math>x</math> be zero and solve the equation for <math>y</math>. | To find <math>y</math>-intercepts, let <math>x</math> be zero and solve the equation for <math>y</math>. | ||
| − | '''Example''' Find the x-intercepts and y-intercepts of the | + | '''Example''' Find the x-intercepts and y-intercepts of the function <math>y=x^2-2x</math> |
{| class = "mw-collapsible mw-collapsed" style = "text-align:left;" | {| class = "mw-collapsible mw-collapsed" style = "text-align:left;" | ||
!Solution: | !Solution: | ||
| Line 65: | Line 65: | ||
|So, <math>r=\sqrt{(2-3)^2+(1-4)^2}=\sqrt{1+9}=\sqrt{10}</math> | |So, <math>r=\sqrt{(2-3)^2+(1-4)^2}=\sqrt{1+9}=\sqrt{10}</math> | ||
|- | |- | ||
| − | |Now, write the equation of the circle with radius <math>r=\sqrt{10}</math> and center <math>(3,4)</math> | + | |Now, write the equation of the circle with radius <math>r=\sqrt{10}</math> and center <math>(3,4)</math> to get: |
| + | |- | ||
| + | |<math>(x-3)^2+(y-4)^2=10</math> | ||
|} | |} | ||
| Line 71: | Line 73: | ||
Distance <math>D</math> between <math>(x_1,y_1)</math> and <math>(x_2,y_2)</math> can be calculated by using <math>D=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}</math> | Distance <math>D</math> between <math>(x_1,y_1)</math> and <math>(x_2,y_2)</math> can be calculated by using <math>D=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}</math> | ||
| + | |||
| + | ==Points of Intersection== | ||
| + | |||
| + | An ordered pair that is a solution of two different equations is called a point of intersection of the graphs of the two equations | ||
| + | |||
| + | For example, find the point(s) of intersection of two equations <math>y=2x-1</math> and <math>y=3x+4</math>. | ||
| + | |||
| + | The order pairs that satisfy both of these equation should have the same <math>y</math> value, so <math>y=2x-1=3x+4</math> | ||
| + | |||
| + | Then, <math>2x-1=3x+4</math> | ||
| + | |||
| + | Therefore <math>x=-5</math> | ||
| + | |||
| + | |||
| + | [[Math_22| '''Return to Topics Page''']] | ||
'''This page were made by [[Contributors|Tri Phan]]''' | '''This page were made by [[Contributors|Tri Phan]]''' | ||
Latest revision as of 06:50, 19 July 2020
The Graph of an Equation
The graph of an equation is the set of all points that are solutions of the equation.
In this section, we use point-plotting method. With this method, you construct a table of values that consists of several solution points of the equation
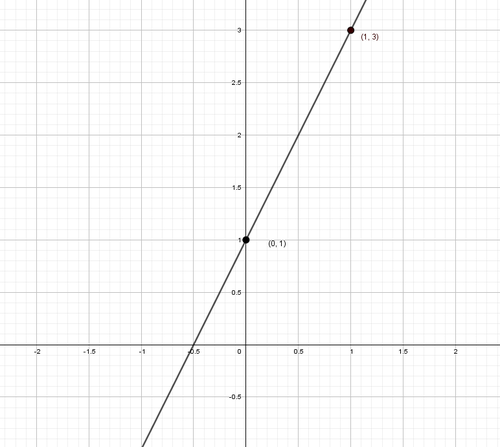
For example, sketch the graph of . We can construct the table below by plugging points for .
| x | 0 | 1 | 2 | 3 |
| y=2x+1 | 1 | 3 | 5 | 7 |
So, we can sketch the graph from those order pairs.
Intercepts of a Graph
Some solution points have zero as either the -coordinate or the -coordinate. These points are called intercepts because they are the points at which the graph intersects the - or -axis.
To find -intercepts, let be zero and solve the equation for . To find -intercepts, let be zero and solve the equation for .
Example Find the x-intercepts and y-intercepts of the function
| Solution: |
|---|
| x-intercept: Let , so , hence , therefore, or |
| y-intercept: Let , so |
| Answer: and are x-intercepts |
| is y-intercept |
Circles
The standard form of the equation of a circle is The point is the center of the circle, and the positive number is the radius of the circle
In general, to write an equation of a circle, we need to know radius and the center .
Example Given that the point is on the circle centered at (3,4). Find the equation of a circle.
| Solution: |
|---|
| We need to know the radius and the center in order to write the equation. The center is given at . It is left to find the radius. |
| Radius is the distance between the center and a point on the circle. So, radius is the distance between and . |
| So, |
| Now, write the equation of the circle with radius and center to get: |
Notes
Distance between and can be calculated by using
Points of Intersection
An ordered pair that is a solution of two different equations is called a point of intersection of the graphs of the two equations
For example, find the point(s) of intersection of two equations and .
The order pairs that satisfy both of these equation should have the same value, so
Then,
Therefore
This page were made by Tri Phan