Difference between revisions of "Math 22 Graph of Equation"
| Line 31: | Line 31: | ||
To find <math>y</math>-intercepts, let <math>x</math> be zero and solve the equation for <math>y</math>. | To find <math>y</math>-intercepts, let <math>x</math> be zero and solve the equation for <math>y</math>. | ||
| + | |||
| + | '''Example''' Find the x-intercepts and y-intercepts of the graph <math>y=x^2-2x</math> | ||
| + | {| class = "mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| + | !Solution: | ||
| + | |- | ||
| + | |'''x-intercept''': Let <math>y=0</math>, so <math>x^2-2x=0</math>, hence <math>x(x-2)=0</math>, therefore, <math>x=0</math> or <math>x=2</math> | ||
| + | |- | ||
| + | |'''y-intercept''': Let <math>x=0</math>, so <math>y=(0)^2-2(0)=0</math> | ||
| + | |- | ||
| + | |'''Answer''': <math>(0,0)</math> and <math>(2,0)</math> are x-intercepts | ||
| + | |- | ||
| + | |<span style="display:inline-block; width: 54px;"></span> <math>(0,0)</math> is y-intercept | ||
| + | |} | ||
'''This page were made by [[Contributors|Tri Phan]]''' | '''This page were made by [[Contributors|Tri Phan]]''' | ||
Revision as of 07:01, 13 July 2020
The Graph of an Equation
The graph of an equation is the set of all points that are solutions of the equation.
In this section, we use point-plotting method. With this method, you construct a table of values that consists of several solution points of the equation
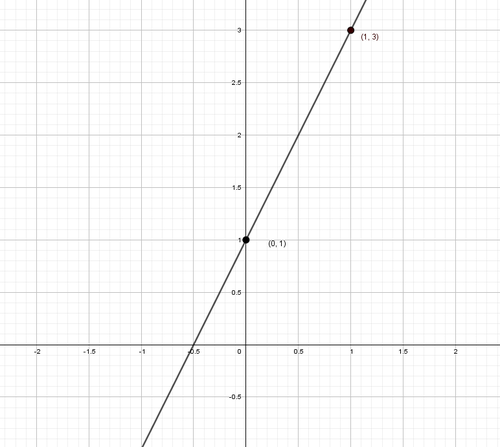
For example, sketch the graph of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=2x+1} . We can construct the table below by plugging points for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} .
| x | 0 | 1 | 2 | 3 |
| y=2x+1 | 1 | 3 | 5 | 7 |
So, we can sketch the graph from those order pairs.
Intercepts of a Graph
Some solution points have zero as either the -coordinate or the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} -coordinate. These points are called intercepts because they are the points at which the graph intersects the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} - or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} -axis.
To find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
-intercepts, let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
be zero and solve the equation for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
.
To find Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
-intercepts, let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
be zero and solve the equation for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y}
.
Example Find the x-intercepts and y-intercepts of the graph Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=x^2-2x}
| Solution: |
|---|
| x-intercept: Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=0} , so Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2-2x=0} , hence Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x(x-2)=0} , therefore, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=2} |
| y-intercept: Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} , so Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=(0)^2-2(0)=0} |
| Answer: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,0)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (2,0)} are x-intercepts |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0,0)} is y-intercept |
This page were made by Tri Phan