Difference between revisions of "009A Sample Final 1, Problem 5"

From Math Wiki
Jump to navigation Jump to search
 
(2 intermediate revisions by the same user not shown)
Line 6: Line 6:
 
!Foundations:    
 
!Foundations:    
 
|-
 
|-
−
|Recall:
+
|'''The Pythagorean Theorem'''
 
|-
 
|-
−
|'''The Pythagorean Theorem:''' For a right triangle with side lengths <math style="vertical-align: -4px">a,b,c</math>, where <math style="vertical-align: 0px">c</math> is the length of the  
+
|&nbsp; &nbsp; &nbsp; &nbsp; For a right triangle with side lengths &nbsp;<math style="vertical-align: -4px">a,b,c</math>&nbsp; where &nbsp;<math style="vertical-align: 0px">c</math>&nbsp; is the length of the  
 
|-
 
|-
 
|
 
|
−
::hypotenuse, we have <math style="vertical-align: -2px">a^2+b^2=c^2.</math>
+
&nbsp; &nbsp; &nbsp; &nbsp; hypotenuse, we have &nbsp;<math style="vertical-align: -2px">a^2+b^2=c^2.</math>
 
|}
 
|}
 +
  
 
'''Solution:'''
 
'''Solution:'''
Line 21: Line 22:
 
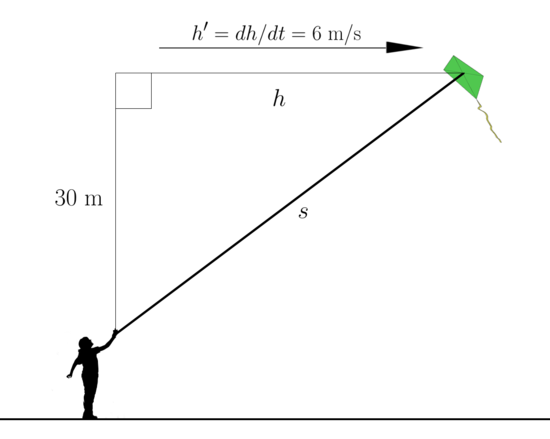
|[[File:9AF_5_GP.png|center|550px]]
 
|[[File:9AF_5_GP.png|center|550px]]
 
|-
 
|-
−
|From the diagram, we have <math style="vertical-align: -3px">30^2+h^2=s^2</math> by the Pythagorean Theorem.
+
|From the diagram, we have &nbsp;<math style="vertical-align: -3px">30^2+h^2=s^2</math>&nbsp; by the Pythagorean Theorem.
 
|-
 
|-
 
|Taking derivatives, we get  
 
|Taking derivatives, we get  
 
|-
 
|-
 
|
 
|
−
::<math>2hh'=2ss'.</math>
+
&nbsp; &nbsp; &nbsp; &nbsp; <math>2hh'=2ss'.</math>
 
|}
 
|}
  
Line 32: Line 33:
 
!Step 2: &nbsp;
 
!Step 2: &nbsp;
 
|-
 
|-
−
|If&thinsp; <math style="vertical-align: -4px">s=50,</math> then&thinsp; <math style="vertical-align: -2px">h=\sqrt{50^2-30^2}=40.</math>
+
|If &nbsp; <math style="vertical-align: -4px">s=50,</math>&nbsp; then
 
|-
 
|-
−
|So, we have&thinsp; <math style="vertical-align: -5px">2(40)6=2(50)s'.</math>
+
|&nbsp; &nbsp; &nbsp; &nbsp;<math style="vertical-align: -2px">h=\sqrt{50^2-30^2}=40.</math>
 
|-
 
|-
−
|Solving for&thinsp; <math style="vertical-align: -5px">s',</math> we get&thinsp; <math style="vertical-align: -14px">s'=\frac{24}{5}</math>&thinsp; m/s.
+
|So, we have
 +
|-
 +
|&nbsp; &nbsp; &nbsp; &nbsp; <math style="vertical-align: -5px">2(40)6=2(50)s'.</math>
 +
|-
 +
|Solving for &nbsp; <math style="vertical-align: -5px">s',</math>&nbsp;  we get &nbsp; <math style="vertical-align: -14px">s'=\frac{24}{5} \text{ m/s.}</math> &nbsp;
 
|}
 
|}
 +
  
 
{| class="mw-collapsible mw-collapsed" style = "text-align:left;"
 
{| class="mw-collapsible mw-collapsed" style = "text-align:left;"
 
!Final Answer: &nbsp;  
 
!Final Answer: &nbsp;  
 
|-
 
|-
−
|
+
|&nbsp; &nbsp; &nbsp; &nbsp;<math style="vertical-align: -14px">s'=\frac{24}{5} \text{ m/s}</math>&nbsp;
−
:<math style="vertical-align: -14px">s'=\frac{24}{5}</math>&thinsp; m/s
 
 
|}
 
|}
 
[[009A_Sample_Final_1|'''<u>Return to Sample Exam</u>''']]
 
[[009A_Sample_Final_1|'''<u>Return to Sample Exam</u>''']]

Latest revision as of 08:12, 10 April 2017

A kite 30 (meters) above the ground moves horizontally at a speed of 6 (m/s). At what rate is the length of the string increasing

when 50 (meters) of the string has been let out?

Foundations:  
The Pythagorean Theorem
        For a right triangle with side lengths    where    is the length of the

        hypotenuse, we have  


Solution:

Step 1:  
9AF 5 GP.png
From the diagram, we have    by the Pythagorean Theorem.
Taking derivatives, we get

       

Step 2:  
If     then
       
So, we have
       
Solving for     we get    


Final Answer:  
        

Return to Sample Exam

Retrieved from "https://wiki.math.ucr.edu/index.php?title=009A_Sample_Final_1,_Problem_5&oldid=1526"