009C Sample Final 1, Problem 10

A curve is given in polar parametrically by

$x(t)=3\sin t$

$y(t)=4\cos t$

$0\leq t\leq 2\pi$

a) Sketch the curve.

b) Compute the equation of the tangent line at $t_{0}={\frac {\pi }{4}}$.

Foundations:
1. What two pieces of information do you need to write the equation of a line?
You need the slope of the line and a point on the line.
2. What is the slope of the tangent line of a parametric curve?
The slope is $m={\frac {dy}{dx}}={\frac {\frac {dy}{dt}}{\frac {dx}{dt}}}.$

Solution:

(a)

Step 1:

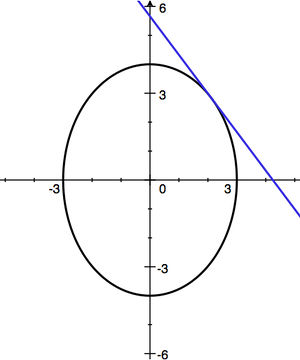
(b)

Step 1:
First, we need to find the slope of the tangent line.
Since ${\frac {dy}{dt}}=-4\sin t$ and ${\frac {dx}{dt}}=3\cos t,$ we have
${\frac {dy}{dx}}={\frac {\frac {dy}{dt}}{\frac {dx}{dt}}}={\frac {-4\sin t}{3\cos t}}.$
So, at $t_{0}={\frac {\pi }{4}},$ the slope of the tangent line is
$m={\frac {-4\sin {\bigg (}{\frac {\pi }{4}}{\bigg )}}{3\cos {\bigg (}{\frac {\pi }{4}}{\bigg )}}}={\frac {-4}{3}}.$

Step 2:
Since we have the slope of the tangent line, we just need a find a point on the line in order to write the equation.
If we plug in $t_{0}={\frac {\pi }{4}}$ into the equations for $x(t)$ and $y(t),$ we get
$x{\bigg (}{\frac {\pi }{4}}{\bigg )}=3\sin {\bigg (}{\frac {\pi }{4}}{\bigg )}={\frac {3{\sqrt {2}}}{2}}$ and
$y{\bigg (}{\frac {\pi }{4}}{\bigg )}=4\cos {\bigg (}{\frac {\pi }{4}}{\bigg )}=2{\sqrt {2}}.$
Thus, the point ${\bigg (}{\frac {3{\sqrt {2}}}{2}},2{\sqrt {2}}{\bigg )}$ is on the tangent line.

Step 3:
Using the point found in Step 2, the equation of the tangent line at $t_{0}={\frac {\pi }{4}}$ is
$y={\frac {-4}{3}}{\bigg (}x-{\frac {3{\sqrt {2}}}{2}}{\bigg )}+2{\sqrt {2}}.$

Final Answer:
(a) See Step 1 above for the graph.
(b) $y={\frac {-4}{3}}{\bigg (}x-{\frac {3{\sqrt {2}}}{2}}{\bigg )}+2{\sqrt {2}}$

Return to Sample Exam