|
|
| Line 1: |
Line 1: |
| | + | [[File:9B_SM3_1_GP.png|right|375px]] |
| | + | |
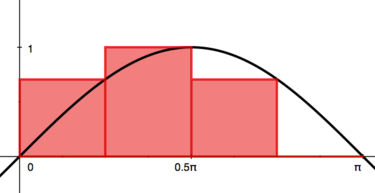
| | <span class="exam">Divide the interval <math style="vertical-align: -5px">[0,\pi]</math> into four subintervals of equal length <math>\frac{\pi}{4}</math> and compute the right-endpoint Riemann sum of <math style="vertical-align: -5px">y=\sin (x).</math> | | <span class="exam">Divide the interval <math style="vertical-align: -5px">[0,\pi]</math> into four subintervals of equal length <math>\frac{\pi}{4}</math> and compute the right-endpoint Riemann sum of <math style="vertical-align: -5px">y=\sin (x).</math> |
| | | | |
Revision as of 14:27, 12 May 2016
Divide the interval ![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751) into four subintervals of equal length
into four subintervals of equal length  and compute the right-endpoint Riemann sum of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\sin (x).}
and compute the right-endpoint Riemann sum of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\sin (x).}
| Foundations:
|
| Recall:
|
- 1. The height of each rectangle in the right-hand Riemann sum is given by choosing the right endpoint of the interval.
|
- 2. See the Riemann sums (insert link) for more information.
|
Solution:
| Step 1:
|
| Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=\sin(x).}
Each interval has length Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{4}.}
|
| So, the right-endpoint Riemann sum of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)}
on the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,\pi]}
is
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{4}\bigg(f\bigg(\frac{\pi}{4}\bigg)+f\bigg(\frac{\pi}{2}\bigg)+f\bigg(\frac{3\pi}{4}\bigg)+f(\pi)\bigg).}
|
| Step 2:
|
| Thus, the right-endpoint Riemann sum is
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{\frac{\pi}{4}\bigg(\sin\bigg(\frac{\pi}{4}\bigg)+\sin\bigg(\frac{\pi}{2}\bigg)+\sin\bigg(\frac{3\pi}{4}\bigg)+\sin(\pi)\bigg)} & = & \displaystyle{\frac{\pi}{4}\bigg(\frac{\sqrt{2}}{2}+1+\frac{\sqrt{2}}{2}+0\bigg)}\\ &&\\ & = & \displaystyle{\frac{\pi}{4}(\sqrt{2}+1).}\\ \end{array}}
|
| Final Answer:
|
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{4}(\sqrt{2}+1)}
|
Return to Sample Exam
![{\displaystyle [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)
