Difference between revisions of "009B Sample Final 1, Problem 5"

From Math Wiki
Jump to navigation Jump to search
Line 3: Line 3:
 
::::::<span class="exam"> <math style="vertical-align: 0px">x=0</math>, <math style="vertical-align: -4px">y=e^x</math>, and <math style="vertical-align: -4px">y=ex</math>.
 
::::::<span class="exam"> <math style="vertical-align: 0px">x=0</math>, <math style="vertical-align: -4px">y=e^x</math>, and <math style="vertical-align: -4px">y=ex</math>.
  
−
<span class="exam">a) Sketch the region bounded by the given three functions. Find the intersection point of the two functions:  
+
::<span class="exam">a) Sketch the region bounded by the given three functions. Find the intersection point of the two functions:  
  
−
:<span class="exam"><math style="vertical-align: -4px">y=e^x</math> and <math style="vertical-align: -4px">y=ex</math>. (There is only one.)
+
::::::<span class="exam"><math style="vertical-align: -4px">y=e^x</math> and <math style="vertical-align: -4px">y=ex</math>. (There is only one.)
  
−
<span class="exam">b) Set up the integral for the volume of the solid.
+
::<span class="exam">b) Set up the integral for the volume of the solid.
  
−
<span class="exam">c) Find the volume of the solid by computing the integral.
+
::<span class="exam">c) Find the volume of the solid by computing the integral.
  
 
{| class="mw-collapsible mw-collapsed" style = "text-align:left;"
 
{| class="mw-collapsible mw-collapsed" style = "text-align:left;"
Line 16: Line 16:
 
|Recall:
 
|Recall:
 
|-
 
|-
−
|'''1.''' You can find the intersection points of two functions, say <math style="vertical-align: -5px">f(x),g(x),</math>
+
|
 +
::'''1.''' You can find the intersection points of two functions, say <math style="vertical-align: -5px">f(x),g(x),</math>
 
|-
 
|-
 
|
 
|
−
::by setting <math style="vertical-align: -5px">f(x)=g(x)</math> and solving for <math style="vertical-align: 0px">x</math>.
+
:::by setting <math style="vertical-align: -5px">f(x)=g(x)</math> and solving for <math style="vertical-align: 0px">x.</math>
 
|-
 
|-
−
|'''2.''' The volume of a solid obtained by rotating an area around the <math style="vertical-align: -4px">y</math>-axis using cylindrical shells is given by   
+
|
 +
::'''2.''' The volume of a solid obtained by rotating an area around the <math style="vertical-align: -4px">y</math>-axis using cylindrical shells is given by   
 
|-
 
|-
 
|
 
|
−
::<math style="vertical-align: -13px">\int 2\pi rh~dx,</math> where <math style="vertical-align: 0px">r</math> is the radius of the shells and <math style="vertical-align: 0px">h</math> is the height of the shells.
+
:::<math style="vertical-align: -13px">\int 2\pi rh~dx,</math> where <math style="vertical-align: 0px">r</math> is the radius of the shells and <math style="vertical-align: 0px">h</math> is the height of the shells.
 
|}
 
|}
  
Line 44: Line 46:
 
!Step 2: &nbsp;
 
!Step 2: &nbsp;
 
|-
 
|-
−
|Setting the equations equal, we have <math style="vertical-align: 0px">e^x=ex</math>.
+
|Setting the equations equal, we have <math style="vertical-align: 0px">e^x=ex.</math>
 
|-
 
|-
−
|We get one intersection point, which is <math style="vertical-align: -4px">(1,e)</math>.
+
|We get one intersection point, which is <math style="vertical-align: -4px">(1,e).</math>
 
|-
 
|-
 
|This intersection point can be seen in the graph shown in Step 1.
 
|This intersection point can be seen in the graph shown in Step 1.
Line 56: Line 58:
 
!Step 1: &nbsp;  
 
!Step 1: &nbsp;  
 
|-
 
|-
−
|We proceed using cylindrical shells. The radius of the shells is given by <math style="vertical-align: 0px">r=x</math>.
+
|We proceed using cylindrical shells. The radius of the shells is given by <math style="vertical-align: 0px">r=x.</math>
 +
|-
 +
|The height of the shells is given by
 
|-
 
|-
−
|The height of the shells is given by <math style="vertical-align: 0px">h=e^x-ex</math>.
+
|
 +
::<math style="vertical-align: 0px">h=e^x-ex.</math>
 
|}
 
|}
  
Line 86: Line 91:
 
|For the first integral, we need to use integration by parts.  
 
|For the first integral, we need to use integration by parts.  
 
|-
 
|-
−
|Let <math style="vertical-align: 0px">u=x</math> and <math style="vertical-align: 0px">dv=e^xdx</math>. Then, <math style="vertical-align: 0px">du=dx</math> and <math style="vertical-align: 0px">v=e^x</math>.
+
|Let <math style="vertical-align: 0px">u=x</math> and <math style="vertical-align: 0px">dv=e^xdx.</math> Then, <math style="vertical-align: 0px">du=dx</math> and <math style="vertical-align: 0px">v=e^x.</math>  
 
|-
 
|-
 
|So, the integral becomes
 
|So, the integral becomes

Revision as of 12:07, 18 April 2016

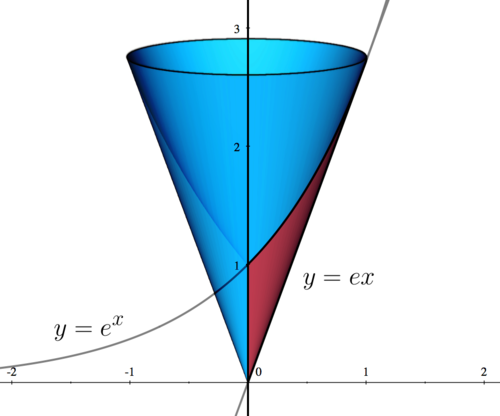
Consider the solid obtained by rotating the area bounded by the following three functions about the -axis:

, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=e^x} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=ex} .
a) Sketch the region bounded by the given three functions. Find the intersection point of the two functions:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=e^x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=ex} . (There is only one.)
b) Set up the integral for the volume of the solid.
c) Find the volume of the solid by computing the integral.
Foundations:  
Recall:
1. You can find the intersection points of two functions, say Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x),g(x),}
by setting Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=g(x)} and solving for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x.}
2. The volume of a solid obtained by rotating an area around the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} -axis using cylindrical shells is given by
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int 2\pi rh~dx,} where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} is the radius of the shells and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h} is the height of the shells.

Solution:

(a)

Step 1:  
First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue.
 
9BF1 5 GP.png
Step 2:  
Setting the equations equal, we have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^x=ex.}
We get one intersection point, which is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,e).}
This intersection point can be seen in the graph shown in Step 1.

(b)

Step 1:  
We proceed using cylindrical shells. The radius of the shells is given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=x.}
The height of the shells is given by
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h=e^x-ex.}
Step 2:  
So, the volume of the solid is
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int 2\pi rh\,dx\,=\,\int_0^1 2\pi x(e^x-ex)\,dx.}

(c)

Step 1:  
We need to integrate
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_0^1 2\pi x(e^x-ex)\,dx\,=\,2\pi\int_0^1 xe^x\,dx-2\pi\int_0^1ex^2\,dx.}
Step 2:  
For the first integral, we need to use integration by parts.
Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dv=e^xdx.} Then, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle du=dx} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=e^x.}
So, the integral becomes
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{\int_0^1 2\pi x(e^x-ex)~dx} & = & \displaystyle{2\pi\bigg(xe^x\bigg|_0^1 -\int_0^1 e^xdx\bigg)-\frac{2\pi ex^3}{3}\bigg|_0^1}\\ &&\\ & = & \displaystyle{2\pi\bigg(xe^x-e^x\bigg)\bigg|_0^1-\frac{2\pi e}{3}}\\ &&\\ & = & \displaystyle{2\pi(e-e-(-1))-\frac{2\pi e}{3}}\\ &&\\ & = & \displaystyle{2\pi-\frac{2\pi e}{3}}.\\ \end{array}}
Final Answer:  
(a)  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,e)} (See Step 1 for the graph)
(b)  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_0^1 2\pi x(e^x-ex)~dx}
(c)  

Return to Sample Exam

Retrieved from "https://wiki.math.ucr.edu/index.php?title=009B_Sample_Final_1,_Problem_5&oldid=1330"