Difference between revisions of "009A Sample Final A, Problem 9"
| Line 16: | Line 16: | ||
!Step 1: | !Step 1: | ||
|- | |- | ||
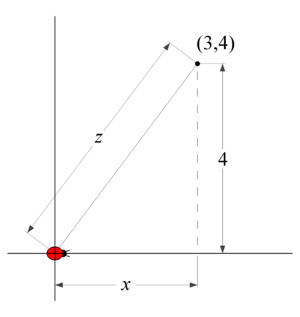
| − | |'''Write the Basic Equation:'''From the picture, we can see there is a triangle involving both the bug and the point (3,4). From this, we can see that <math style="vertical-align: - | + | |'''Write the Basic Equation:'''From the picture, we can see there is a triangle involving both the bug and the point (3,4). From this, we can see that <math style="vertical-align: -10%;">z^2 = x^2 +4^2.</math> |
|} | |} | ||
Revision as of 21:42, 23 March 2015
9. A bug is crawling along the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
-axis at a constant speed of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=30}
.
How fast is the distance between the bug and the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3,4)}
changing
when the bug is at the origin? (Note that if the distance is decreasing, then you should have a negative answer).
| Foundations: |
|---|
| Like most geometric word problems, you should start with a picture. This will help you declare variables and write meaningful equation(s). In this case, we will have to use implicit differentiation to arrive at our related rate. In particular, we need to choose variables to describe the distance between the bug and the point (3,4), which we can call z. By the given information, we can consider the position on the x-axis simply as x. |
Solution:
| Step 1: |
|---|
| Write the Basic Equation:From the picture, we can see there is a triangle involving both the bug and the point (3,4). From this, we can see that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z^2 = x^2 +4^2.} |