Difference between revisions of "009A Sample Final 1, Problem 5"

Revision as of 11:09, 18 April 2016

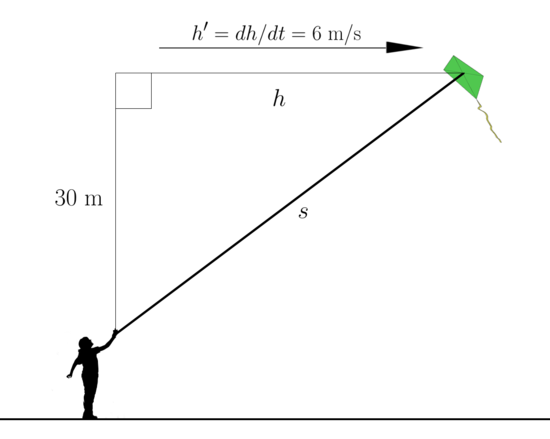
A kite 30 (meters) above the ground moves horizontally at a speed of 6 (m/s). At what rate is the length of the string increasing

when 50 (meters) of the string has been let out?

Foundations:
Recall:
The Pythagorean Theorem:
For a right triangle with side lengths $a,b,c$ , where $c$ is the length of the
hypotenuse, we have $a^{2}+b^{2}=c^{2}.$

Solution:

Step 1:

From the diagram, we have $30^{2}+h^{2}=s^{2}$ by the Pythagorean Theorem.
Taking derivatives, we get
$2hh'=2ss'.$

Final Answer:
$s'={\frac {24}{5}}$ m/s

@@ Line 8: / Line 8: @@
 |Recall:
 |-
-|'''The Pythagorean Theorem:''' For a right triangle with side lengths <math style="vertical-align: -4px">a,b,c</math>, where <math style="vertical-align: 0px">c</math> is the length of the
+|
+::'''The Pythagorean Theorem:'''
+|-
+|
+::For a right triangle with side lengths <math style="vertical-align: -4px">a,b,c</math>, where <math style="vertical-align: 0px">c</math> is the length of the
 |-
 |
@@ Line 32: / Line 36: @@
 !Step 2: &nbsp;
 |-
-|If&thinsp; <math style="vertical-align: -4px">s=50,</math> then&thinsp; <math style="vertical-align: -2px">h=\sqrt{50^2-30^2}=40.</math>
+|If&thinsp; <math style="vertical-align: -4px">s=50,</math> then
 |-
-|So, we have&thinsp; <math style="vertical-align: -5px">2(40)6=2(50)s'.</math>
+|
+::<math style="vertical-align: -2px">h=\sqrt{50^2-30^2}=40.</math>
 |-
-|Solving for&thinsp; <math style="vertical-align: -5px">s',</math> we get&thinsp; <math style="vertical-align: -14px">s'=\frac{24}{5}</math>&thinsp; m/s.
+|So, we have
+|-
+|
+::<math style="vertical-align: -5px">2(40)6=2(50)s'.</math>
+|-
+|Solving for&thinsp; <math style="vertical-align: -5px">s',</math> we get
+|-
+|
+::<math style="vertical-align: -14px">s'=\frac{24}{5}</math>&thinsp; m/s.
 |}