Difference between revisions of "009A Sample Final 1, Problem 7"
Jump to navigation
Jump to search
(Created page with "<span class="exam">A curve is defined implicitly by the equation ::::::<math>x^3+y^3=6xy.</math> <span class="exam">a) Using implicit differentiation, compute <math...") |
|||
| Line 78: | Line 78: | ||
| | | | ||
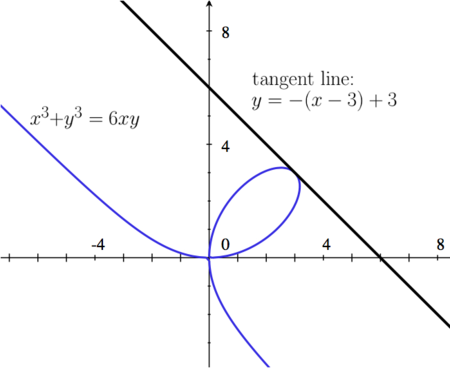
::<math>y\,=\,-1(x-3)+3.</math> | ::<math>y\,=\,-1(x-3)+3.</math> | ||
| + | |- | ||
| + | ||[[File: 9AF1_7_GP.png |center|450px]] | ||
|} | |} | ||
Revision as of 23:19, 4 March 2016
A curve is defined implicitly by the equation
a) Using implicit differentiation, compute .
b) Find an equation of the tangent line to the curve at the point .
| Foundations: |
|---|
| 1. What is the result of implicit differentiation of |
|
| 2. What two pieces of information do you need to write the equation of a line? |
|
| 3. What is the slope of the tangent line of a curve? |
|
Solution:
(a)
| Step 1: |
|---|
| Using implicit differentiation on the equation we get |
|
|
| Step 2: |
|---|
| Now, we move all the terms to one side of the equation. |
| So, we have |
|
|
| We solve to get |
(b)
| Step 1: |
|---|
| First, we find the slope of the tangent line at the point |
| We plug into the formula for we found in part (a). |
| So, we get |
|
|
| Step 2: |
|---|
| Now, we have the slope of the tangent line at and a point. |
| Thus, we can write the equation of the line. |
| So, the equation of the tangent line at is |
|
|
| Final Answer: |
|---|
| (a) |
| (b) |