Difference between revisions of "009B Sample Final 1, Problem 5"
Jump to navigation
Jump to search
(Created page with "<span class="exam"> Consider the solid obtained by rotating the area bounded by the following three functions about the <math style="vertical-align: -3px">y</math>-axis: ::::...") |
|||
| Line 34: | Line 34: | ||
!Step 1: | !Step 1: | ||
|- | |- | ||
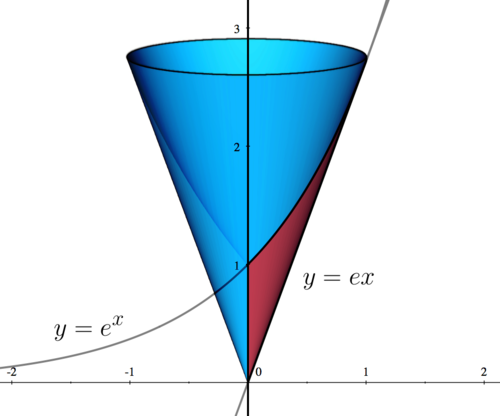
| − | |First, we sketch the region bounded by the three functions. | + | |First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue. |
|- | |- | ||
| − | | | + | |[[File:9BF1 5 GP.png|center|500px]] |
|} | |} | ||
Revision as of 21:56, 26 February 2016
Consider the solid obtained by rotating the area bounded by the following three functions about the -axis:
- , , and .
a) Sketch the region bounded by the given three functions. Find the intersection point of the two functions:
- and . (There is only one.)
b) Set up the integral for the volume of the solid.
c) Find the volume of the solid by computing the integral.
| Foundations: |
|---|
| Recall: |
| 1. You can find the intersection points of two functions, say |
|
| 2. The volume of a solid obtained by rotating an area around the -axis using cylindrical shells is given by |
|
Solution:
(a)
| Step 1: |
|---|
| First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue. |
| Step 2: |
|---|
| Setting the equations equal, we have . |
| We get one intersection point, which is . |
| This intersection point can be seen in the graph shown in Step 1. |
(b)
| Step 1: |
|---|
| We proceed using cylindrical shells. The radius of the shells is given by . |
| The height of the shells is given by . |
| Step 2: |
|---|
| So, the volume of the solid is |
|
|
(c)
| Step 1: |
|---|
| We need to integrate |
|
|
| Step 2: |
|---|
| For the first integral, we need to use integration by parts. |
| Let and . Then, and . |
| So, the integral becomes |
|
|
| Final Answer: |
|---|
| (a) (See Step 1 for the graph) |
| (b) |
| (c) |